My truth and your truth
We live in an age when everybody seems to have their personal truth. Both influencers and politicians love to proclaim to ‘live their own truth’ and suggest you do the same.
Check this video, for example:
It is not clear what these people mean by ‘truth’. It seems to me that, in modern parlance, truth is a synonym of ‘authenticity,’ so when they say ‘live your truth’ they simply mean ‘be authentic.’
There’s nothing wrong with that. Of course, you should be authentic and accept yourself (provided that being yourself does not harm others). But, I wish they would simply say that instead of coating their claims with the term ‘truth.’
The thing is, the concept of truth is already quite complex. There’s a lot of ambiguity around it and confusing it with yet another idea isn’t helpful.
Let’s not be influencers today. Let’s stop confusing truth with authenticity. Instead, let’s discuss the concept of truth, and see if we can make any sense of it.
So, what is truth?
Of course, philosophers have many theories
Well, there’s no simple answer, that’s obvious. One can go the easy route and proclaim that there is no such thing as objective truth, so it’s pointless to even try answering the question. That’s the relativist perspective, and I honestly think it is intellectually lazy. Truth is both an interesting and important concept, and we should do better in trying to understand it.
In philosophy - the primary discipline asking questions about the nature of truth - there are several theories about truth. Each of them offers a somewhat different answer.
Here are four interesting ones:
Correspondence theory says that a statement is true if it accurately reflects the real world. In other words, truth is about your statements matching up with (corresponding to) facts or events. Think of it like a mirror - if what you say reflects reality, then it is true.
Coherence theory suggests that a belief is true if it fits well within a consistent system of beliefs. It’s like a puzzle; if your belief clicks into place without contradicting other pieces (other beliefs in the system), it is true.
Formal theory defines truth in terms of proper logical connections between sentences. If one claim follows from others, then it is true. It’s very similar to math. Imagine a mathematical equation where everything needs to balance perfectly.
Deflationist theory sees the truth as a trivial property of definitions that imply themselves. For example, “Bachelors are unmarried” is true because the definition of being a bachelor implies being unmarried.
There are several others, of course. Philosophers are a garrulous bunch; they like to talk and invent endless debates about definitions. If you’re interested in learning more, see here.
Despite differences in the definition of truth, there are also some commonalities. In particular, there’s one glaring thing they all share:
All of them imply that truth has something to do with order.
The correspondence theory emphasizes a matching order; the coherence theory implies contextual order; the formal theory depends on the order of connections between claims; and the deflationist theory depends on ordered definitions.
This is not an accident. Whatever your idea of truth is, there has to be some order and structure behind it.
Instead of subscribing to some particular philosophical theory of truth, let’s focus on the idea that truth depends on order.
Truth and order
Here’s a funny thing about order: it is totalitarian (that’s why you don’t want to have too much of it in a society). When things are ordered, they belong to a vertical hierarchy of other ordered things; everything must have its place in the system.
First, at the most basic level, for truth to be possible, the ways of expressing it must be ordered in some way. Since at the most basic level we use language to express truth, this means that language needs to follow some order and structure.
We call such order logic.
Language and meta-language
To understand logic, we need to make a distinction between the different ways we can use language. Things can get tricky here because language is a very slippery phenomenon; it easily escapes our grasp.
At the most basic level, we use language to describe the world. When we see a flower, we use the word ‘flower’ to refer to it.
However, we can also use language to describe and refer to language. We can say, for example, that ‘flower’ is a word in English describing the reproductive part of a plant that people like to have in their garden. In this case, we used meta-language, the language describing language (‘meta’ is Greek for beyond).
We can go higher in abstraction, and say that the sentence:
We can say, for example, that ‘flower’ is a word in English describing the reproductive part of a plant that people like to have in their garden.
is a sentence describing how language describes reality. This would be meta-meta-language.
We can go on and on. But, we won’t.
The important thing to understand is that logic is like a meta-language. It is a way we clarify how language can be used to help us recognize, discover, and communicate truth. It’s like an external perspective on what we express by language; a bird’s-eye view of language, if you will.
Truth as a function
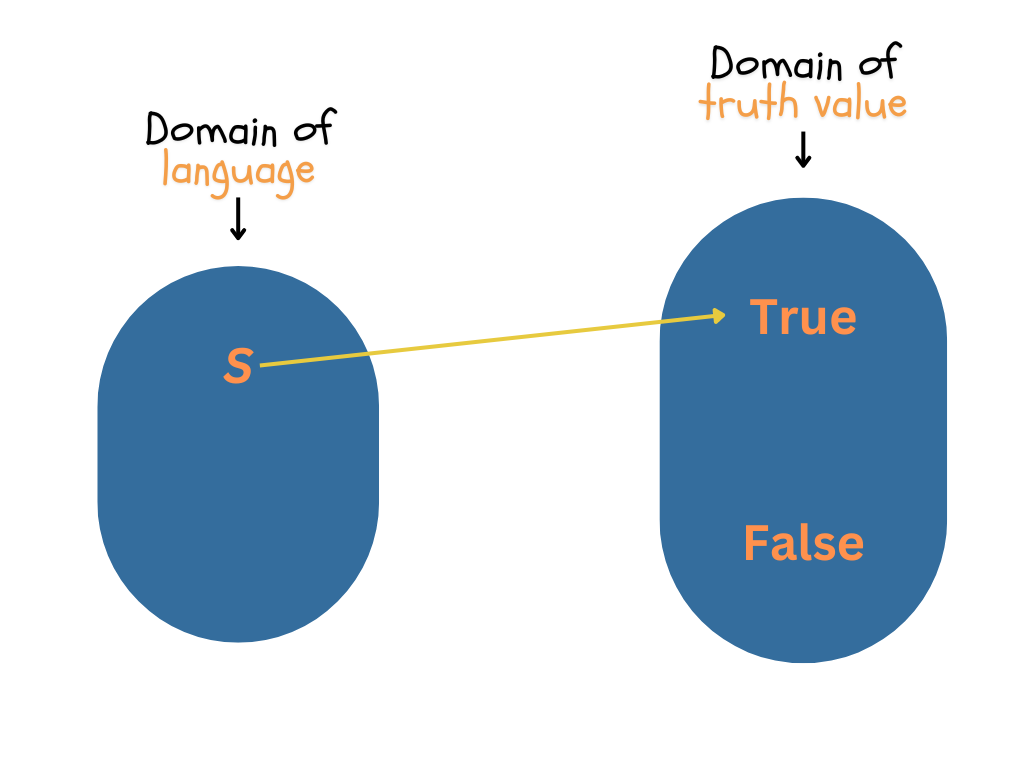
Another useful way to conceptualize truth is to think about truth as a function. If you remember the last lesson, functions are maps between two domains, the domain of input and the domain of output.
What logic helps us do is to make a map between the domain of language (as input) and the domain of truth value (True and False) as output. When we say that some sentence S (where S is a symbol for a whole sentence) is true, we are saying that the sentence S is mapped to True, like this:
So, at the most basic level, truth is a function assigning each sentence an output in the domain of truth value. Logic helps us specify this function in more detail.
Depending on how complex the things we have to say are, there are different types of logic. Some of them are less, and some are more ‘granular’; that is, they allow us to break down language into smaller or larger logical components.
Imagine logic was a camera on your smartphone. If the phone is old, the images made on it will have very low resolution; if it’s new, the resolution will be much better. Similarly, early types of logic had a low ‘resolution’, they were not granular enough, while the newer ones offered more detail in how they represented our use of language for dealing with truth.
There are several types of logic (hence a more appropriate term would be logics). Here are three popular ones:
Propositional logic is known to be the simplest form of logic. It deals with propositions and their mutual relationships. ‘Proposition’ is a name we use in logic for particular kinds of sentences (‘statement’ is a synonym). We recognize them because they can be either true or false. For example,
It is raining.
is a basic proposition. We can denote it by a single letter R. It is either true or false. Right now, it is either raining, or it is not raining. Either R is true, or not R is true.
On the other hand,
Why is it not raining?
is not a proposition because it lacks the true-or-false feature. We are not stating that anything is true here. Questions, commands, or other kinds of sentences that lack this feature are not propositions. So, propositions are a subset of sentences; not every sentence is a proposition, while every proposition is a sentence.
Propositions can be basic like the one just mentioned, or they can be more complex. We can put two (or more) basic propositions together and use logical connectives (like AND, OR, NOT, IF→THEN) to make compound propositions, like these:
It is raining AND today is Tuesday.
It is NOT raining.
IF it is raining, THEN there are clouds.
Exercise 1: Make five basic propositions. Then use them together with the logical connectives to make five compound propositions.As you can see, propositional logic can help us think about truth in a way similar to the correspondence theory of truth. We can consider a sentence true only if two requirements are satisfied:
First, the sentence has truth value - it can be either true or false,
Second, the sentence maps to true.
The first requirement is easier to satisfy, of course. However, the second one is not satisfied so easily. It is hard to know if some sentence S is true.
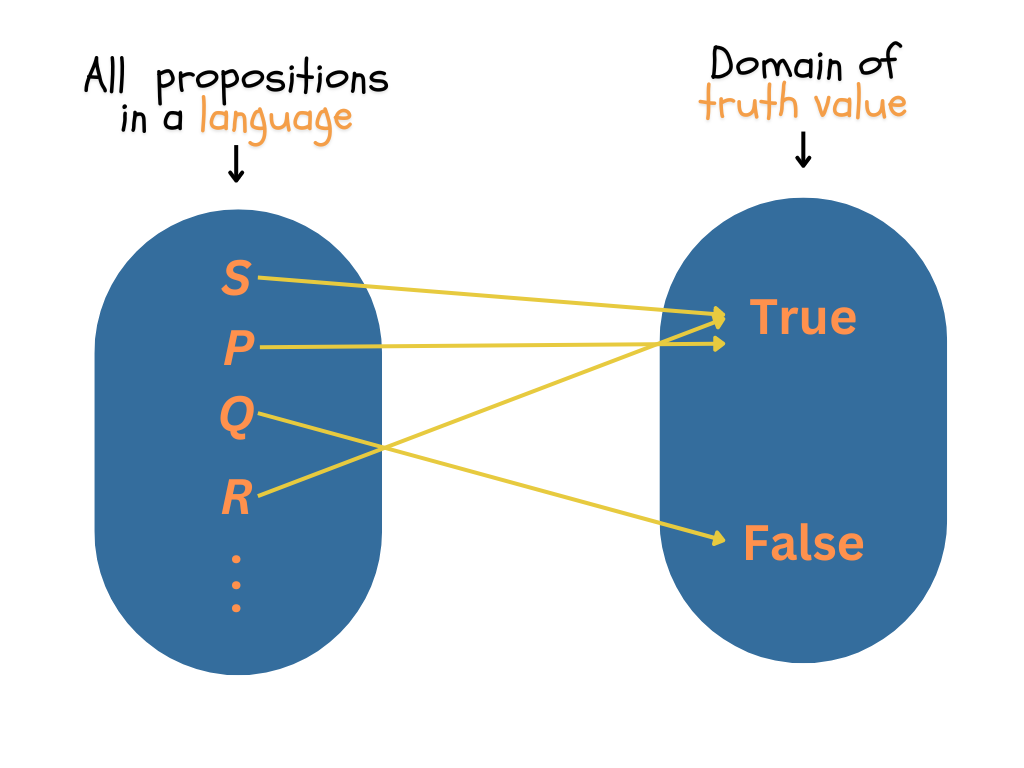
In an ideal world, if we could list all possible propositions in English (including all possible combinations of them using logical connectives), and denote them by symbols like S, P, Q, R, and similar, then we could make a complete mapping between the domain of all propositions and the domain of truth value, where each proposition would either be true or false.
It would look something like this:
In such a world, we would know if any sentence is true.
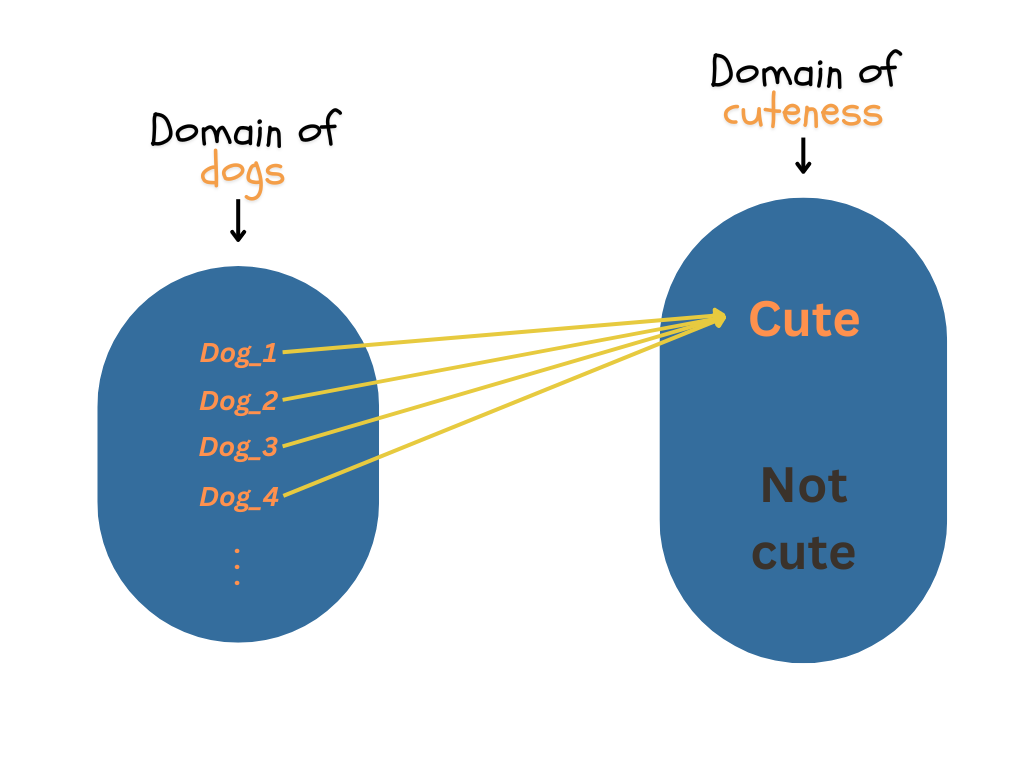
However, we don’t live in an ideal world. Reality is more complex than can be modeled using propositional logic because propositional logic is very rough. It looks more like this picture:
While it can be helpful for some things (as you will see in future lessons), we need something more granular, and realistic.
Predicate logic extends propositional logic by adding subjects, predicates, and quantifiers. In logic, the words ‘subject’ and ‘predicate’ are similar to their meaning in linguistics. A predicate is a property or a relation that is attributed to subjects.
For example, in a sentence:
Fluffy is cute.
‘is cute’ is a predicate of the subject Fluffy.
Quantifiers are words such as ‘all’, ‘none’, or ‘some’ that specify the extent to which predicates apply (how many subjects they cover).
For example, in a sentence:
All dogs are cute.
the word ‘All’ is a quantifier. It tells us that the predicate ‘is cute’ applies to all dogs. This is a more granular representational system because it gives us more ‘knobs’ to tune when describing the world.
Since predicate logic is an extension of propositional logic (which means it takes over its rules and adds more), we can make compound propositions using predicates and quantifiers, together with other logical operators, like this:
All dogs are cute, AND no cats are cute.
IF all dogs are cute, AND Fluffy is a dog, THEN Fluffy is cute.
Exercise 2: Make five basic propositions using one predicate and one quantifier. Then, make five compound propositions using the same predicates and quantifiers.Predicate logic gets us to a position where we can express more detailed descriptions of the world while keeping our representational system ordered. Instead of just propositions, we have elements that make them: subjects, predicates, and quantifiers.
The image now looks like this:
Finally, modal logic introduces the concepts of necessity and possibility into logical analysis. It extends predicate logic by giving us the tools to distinguish between statements that are true by necessity, or by possibility.
Thus, we can say that the sentence “Bachelors are unmarried” is true by necessity, while the sentence “It will rain tomorrow” is true by possibility. The former sentences must be true, while the latter ones can, but don’t have to.
Exercise 3: Write five sentences that are necessarily true, and five sentences that are possibly, but not necessarily true.If you like to ponder about the multiverse, you’ll like modal logic because it uses terms such as possible worlds. It imagines that there’s not just a single world out there, but infinitely many of them.
For example, there is a world in which today is Tuesday and another one in which today is Sunday (and one for each day of the week). Statements that are true in all of these possible worlds are necessary truths, while those true only in some of them are possible truths. “2+2=4” is a necessary truth, while “Teachers are cool” is a possible truth.
Types of truth
We are finally in the position to make some claims about what kinds of truth-bearing statements (propositions claimed to be true) there are and how to recognize and evaluate them.
To do so, we will use a nifty logical mechanism called the square of opposition. This graph describes different kinds of statements and their truth claims.
Follow the picture below to follow the distinctions.
There are:
Universal Affirmative statements (top left corner), which claim that all subjects (S) have property (P). These are propositions such as “All dogs are cute,” “All articles on Substack are fun,” and similar. Also called type A statements (hence SaP below the top left diagram).
Universal Negative statements (top right corner) make a contrary claim, saying that no subject (S) has the property (P). Examples would be: “No dogs are cute,” or “No article on Substack is fun.” Also called type E statements (hence SeP below the top left diagram).
Particular Affirmative (bottom left) statements claim that some subjects (S) have property (P). These are propositions like “Some dogs are cute,” or “Some people have beards.” Also called type I statements (hence SiP below the top left diagram).
Particular Negative (bottom right) statements, which claim that some subjects (S) do not have property (P). Examples are: “Some dogs are not cute,” or “Some people don’t have beards.” Also called type O statements (SoP below the top left diagram).
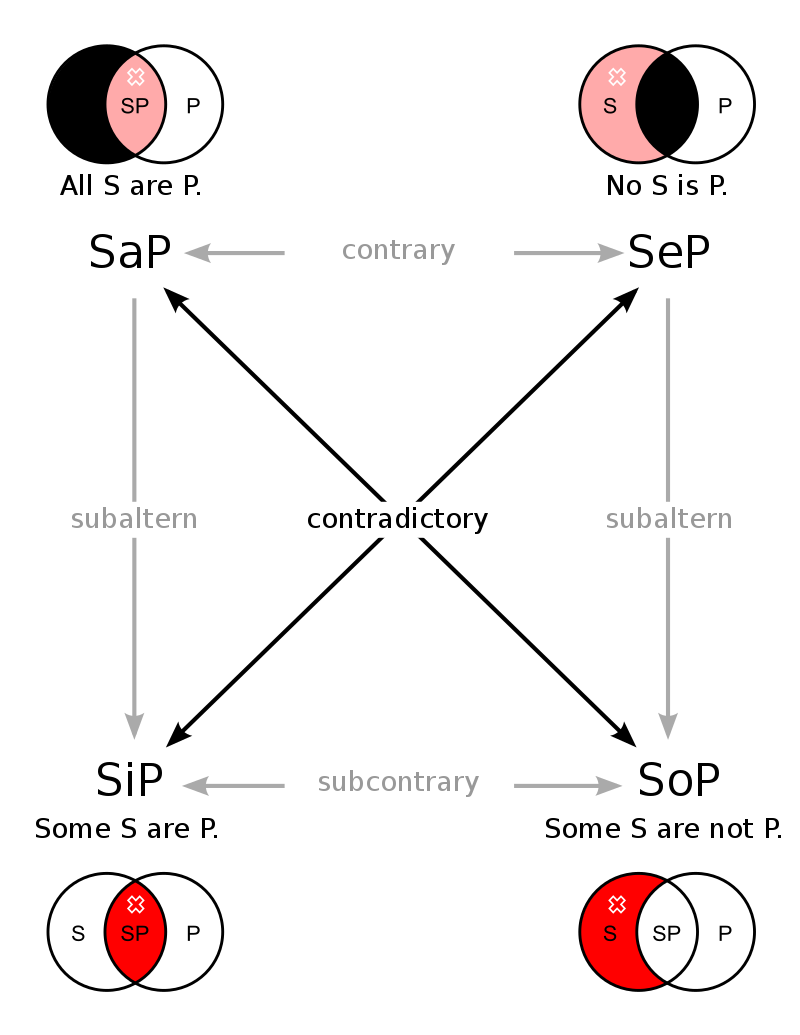
The most basic generalization we can make based on this square is the one distinguishing claims implying certainty and those implying probability.
The top of the square (SaP and SeP) includes claims of certainty. When we say “All dogs are cute” we wish to suggest that there are no exceptions to this claim; there is not a single dog that is not cute; it is necessary that all of them are.
As a function, a Universal Affirmative claim looks like this:
Certainty is achieved because every element of the input domain is matched with a single element of the output domain.
We can also see how this claim relates to corresponding claims in the square of opposition. Looking at the top two types (SaP and SeP) we see that they are opposites of one another; one is a mirror image of the other, and they cannot both be true. That is because necessities are exclusive.
Looking at the left side (top and bottom, SaP and SiP), we see that they have an implying relationship, which means that if the top claim is true, then so is the bottom one. “All dogs are cute” implies that “Some dogs are cute” by definition. The same type of relationship goes for the right side, where “No dogs are cute” by definition implies that some of them are not cute. In other words, necessity implies possibility, but not vice versa.
I’m sure you feel a bit awkward now because when you read a claim “Some dogs are cute” you think it implies that some of them aren’t. But, it doesn’t. There is no necessary relationship of implication between the two types at the bottom of the square. If the only thing you know is that “Some dogs are cute,” it does not necessarily follow that some of them aren’t; since you don’t know enough to make a universal statement of either kind, both options are possible: that some dogs are not cute, and that all of them are cute.
What confuses you is the fact that, unlike the top two claims, the bottom two can both be true at the same time. Namely, it can be true that some dogs are cute and some are not. But, they cannot both be false at the same time.
In this case, we can have just one function to represent both particulars, affirmative and negative:
Entropy and truth
The main distinguishing characteristic of the bottom two types (SiP and SoP) is that they guarantee no certainty. Saying “Some dogs are cute” doesn’t give you as much information as saying “All dogs are cute.” If you knew that the latter claim was true, you’d know much more about the world and would be able to make predictions about dogs much more successfully than if the second claim was true.
In that sense, the bottom two claim types have more entropy in them. You can confirm it even visually: the functions for the top two claims are much neater and more ordered than the function for the bottom two.
Truth and computation
To conclude this discussion about truth, let’s see what this lesson's implementation in Python shows us. Go to your Google Colab, open a notebook, and follow along.
First, let’s think about what data type we should use to represent the relationship between the subject and the predicate. If you recall the lesson about Python, dictionaries are useful data types because they allow us to map some elements (keys) to certain values. In our case, the keys would be the names of some group of dogs and the values would be “Cute” and “Not Cute.”
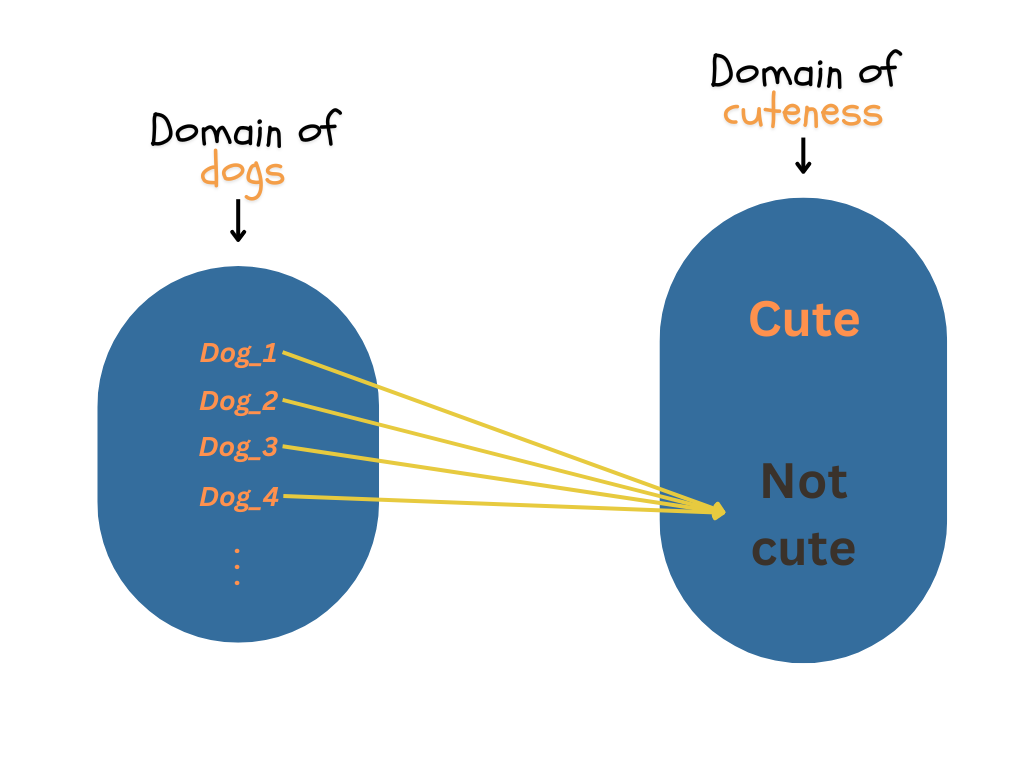
Let’s imagine a dog shelter in which every dog is cute like this:
In this case, we have full information about all dogs, there is no entropy (uncertainty) about the cuteness status of these dogs.
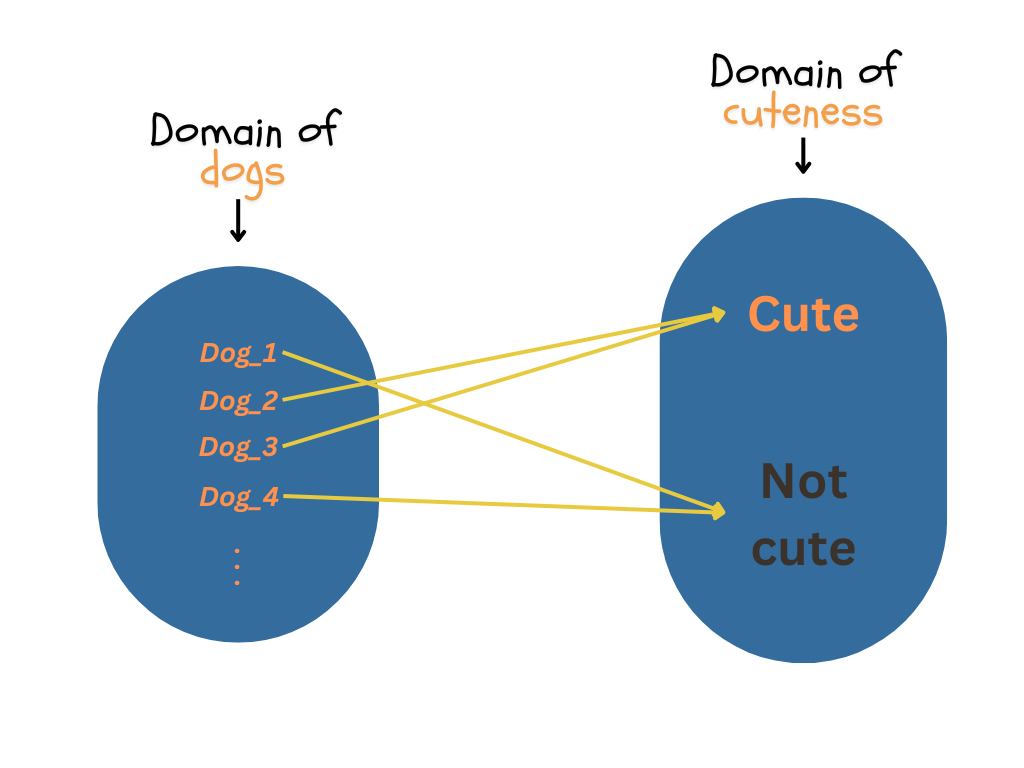
Similarly, let’s model a shelter in which there is no such certainty, like this:
Here, you’ll notice that I first had to import a library called random, because I wanted to model a situation in which the cuteness status of a dog was not guaranteed. The random.choice() method chooses randomly between options we input inside (if you don’t specify otherwise, options we put have an equal probability of being chosen). Here, the two choices, “Cute” and “Not cute” are represented within a list inside the method.
Now, imagine you’re adopting a dog over the phone, and you don’t see any dogs or their photos. Which shelter would you choose if you wanted a cute dog?
It is even trivial to claim that your chances of adopting a cute dog are greater in the first shelter than in the second one, but let’s compute this to verify and think about it more formally.
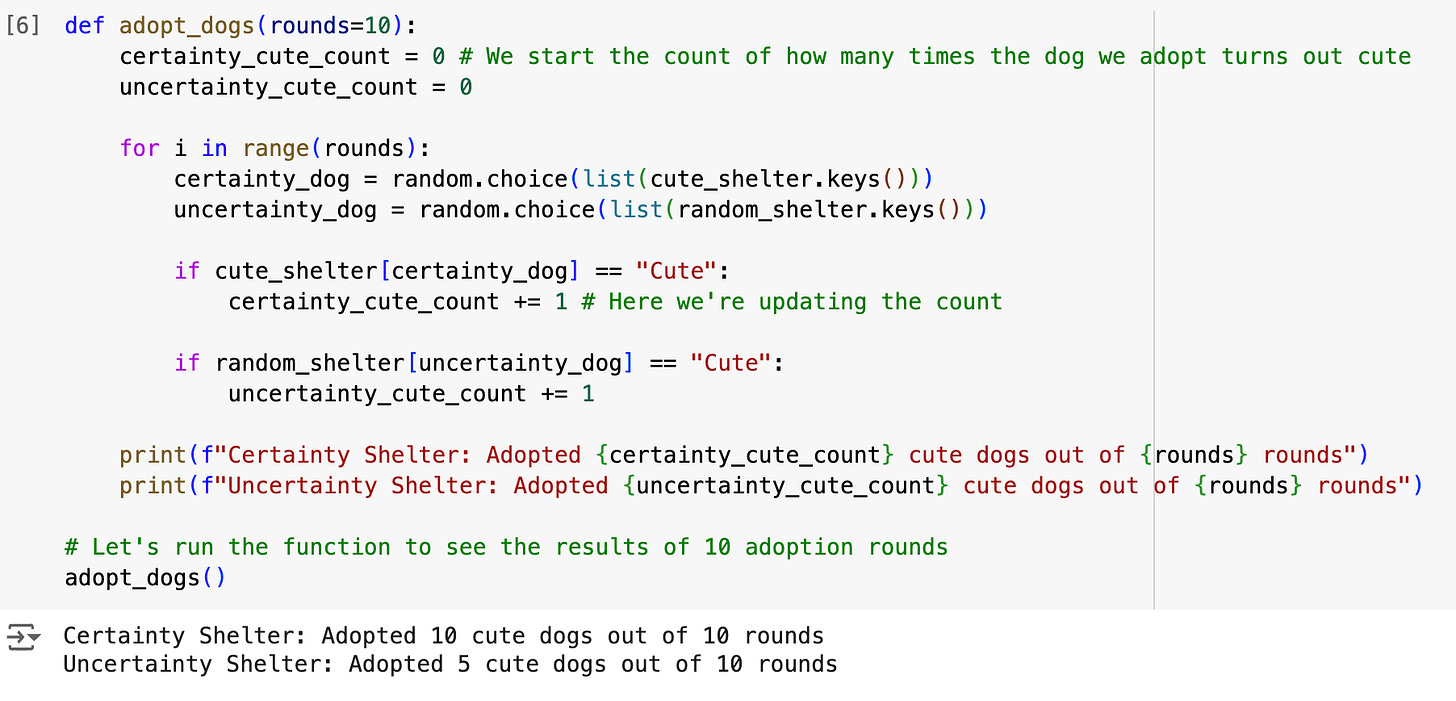
Below I make the function adopt_dogs(rounds=10) that makes 10 hypothetical rounds of dog adoptions and outputs how many of those turned out to be cute. The function adds two new things to what you’ve learned in the previous lesson:
First, the count of some variables. In the first two lines, I set the count of hypothetical cute dogs to 0 (for both shelters), and then I update it by using += 1 operator which adds one to the existing count.
Second, I use a loop, which has a form like this:
for i in range(rounds):
some code that loops through the number of roundsThis is called a for loop and it allows us to perform some operation for a given number of rounds. The i in the first line is a looping variable, which hops over each round in the loop.
As you can see below, this loop first chooses a dog's cuteness status from each shelter’s list of keys using the random.choice method (it calls it certainty_dog if it comes from the cute shelter and uncertainty_dog if it comes from the other one) and then uses the IF→THEN operator to check if the value of that dog is “Cute” or “Not Cute.” If it is cute, then it adds one to the certainty_cute_count, and if not, it adds one to the uncertainty_cute_count.
Finally, it uses an f-string to print out how many cute dogs we get in each scenario.
Exercise 4: What happens if we increase the number of rounds in this function? Increase it to 100 and see if you can predict the number of cute dogs from the uncertainty shelter. Bonus question: What happens when you change the probabilities of each dog being cute or not? Hint: You can do so by changing the method fromrandom.choice()torandom.choices()providing two numbers (that sum to one) inside the method as weights, like this:"Bella": random.choices(["Cute", "Not Cute"], weights=[0.7, 0.3])
Modeling reality like this allows us to see how much of the world is knowable. In cases in which Universal Affirmative or Universal Negative claims are the most appropriate, all of the world described is knowable, and there is no mystery or uncertainty. If we know that “All men are mortal” and that “Socrates is a man,” then we have no doubts that he is mortal too.
But, in the other two cases, we lack such knowledge. The entirety of the world escapes our grasp and we can only guess.
The question then becomes: how do we know our guess is good?
This is where the four philosophical theories we listed at the beginning cannot help us. Faced with uncertainty, we have to find other methods to evaluate our guesses about reality. To do so we have to leave the domain of deterministic logic and enter the domain of a probabilistic one. But, that is a topic for another day.
However, this little dog adoption exercise, though very simple, opens up an interesting question to ponder. Namely, is it possible to always compute truth?
That is, in case we had unlimited computing power and the skills of the best programmers in the world, could we always come up with some procedure that would allow us to find out an answer whether some claim was true or not?
Conclusion
To understand truth, we must first realize the role of order and structure in truth-bearing claims. There can be different kinds of claims to truth, and they differ in scope and the level of confidence they give us in our beliefs. These claims relate to other claims in their conceptual environment in specific and orderly ways, and understanding these relations is also crucial.
As any other philosophical concept, truth is not simple, and will never be. But by caring about order and structure, we can bring some simplicity to claims aspiring to be true and become better at evaluating how successful they are in describing the world to us.
So, don’t give up on truth.







Loved it! I can see Gödel, Turing, and maybe even Tarski raising their hands...