Why You Must Know About Functions
Even if you suck at math
How to get high on functions
In an iconic YouTube video, Thomas Garrity, professor of mathematics at Williams College, his voice breaking from ecstatic excitement, on the border of tears (it seems) opens up his math lecture by telling his students that ‘functions describe the world.’
Everything is described by functions. The sound of my voice on your eardrum - function; the light that is hitting your eyeballs right now - function … It’s aaaall function! Different areas in mathematics study different kinds of functions! High-school math studies second-degree one-variable polynomials! Calculus studies smooth one-variable functions! And it goes on and on!
Functions describe the world!
I really like this clip, I could play it like a song several times a day.
Check it out for yourself:
This clip is a part of his lecture entitled ‘Mathematical Maturity, in which he talks to math teachers about how to understand and recognize mathematical ability in students. It’s not about functions, at least not directly, but the fact that he talks about them in this way suggests something fundamental: understanding functions is important.
This is not a mathematical article. I am no mathematician and I don’t wish to lecture you about different kinds of functions in math. You can relax.
However, being a philosopher and a professor of critical thinking, my job is to focus on ideas and concepts that are useful for understanding the world around us. The idea of a function is among the most important (and underrated) critical thinking concepts, and I will show you why.
What is a function?
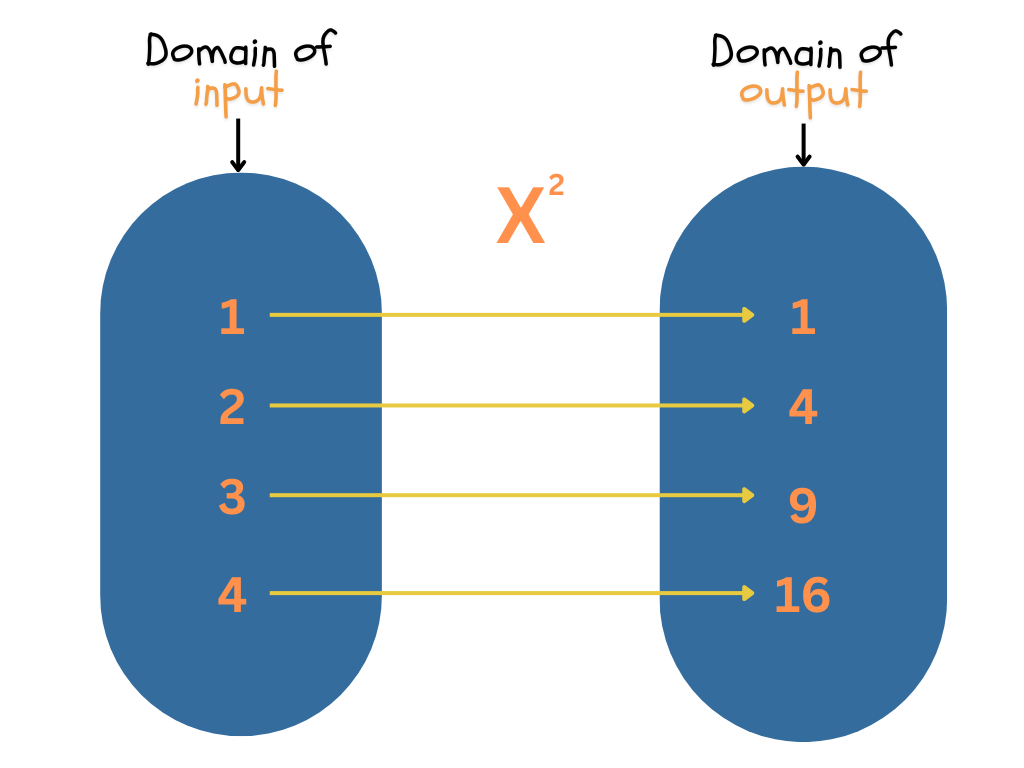
If you’re a student in the US, you’re most likely to learn about functions in middle school. There, they are defined as relationships between sets of numbers, where each input is associated with exactly one output. For example:
is a square function that takes any number as its input (x is a variable that stands for any number), and returns its square as output. If you take 4 as input, you will get 16 as output.
Simple as apple pie.
If we think a bit about functions, we’ll notice some interesting things about their structure. First, functions are like connections between the worlds: the world of input and the world of output. They are like magical doors that connect one domain with another.
Here’s how the simple squaring function looks like a graph:
In mathematical (and some other) parlance, we say that the output is a function of the input. So, 9 is a function of 3, or 16 is a function of 4, where the function is the square.
Functions (in math and elsewhere) are human inventions. When defining them, we get to decide what will go in the domain of input, as well as what the function will do to that input.
This is the second interesting thing about functions: they do things to inputs. In other words, they transform the inputs into something new by mapping them to certain outputs.
While we have freedom in defining what they do, our functions will make sense if the mappings (the connections between the domains of input and output) are meaningful, i.e. if there is some reason certain input gets transformed into certain outputs.
As long as this requirement is satisfied, we can come up with any function, even a silly one like this:
Here, the (unnamed) function connects the great US presidents to dog breeds. Washington is mapped to a Great Dane because Great Danes are believed to be large, strong, and noble dogs, reflecting Washington’s towering role as the first president of the United States. Lincoln is mapped to a Bloodhound because they symbolize persistence and intelligence, qualities that Lincoln exemplified. Roosevelt is mapped to Bull Terriers because they are known for their spirited and adventurous nature.
Exercise 1: Define a function to connect any two domains of your choice. Draw a graph to show it. Write a short explanation about how the domains are connected.This is completely bonkers, I know.
Fortunately, functions play a much more serious role in all domains of science. Every serious inquiry into our reality will make use of functions because they help us model all possible interactions in the world. Reality is complex, and we need conceptual mechanisms to grasp the underlying structures and relationships in various contexts.
Functions do that for us.
Types of functions
Before I show you more examples, let’s see what different kinds of functions we can have. We can categorize functions based on the nature of the relationship between the inputs and outputs.
Here are a few important types:
One-to-one
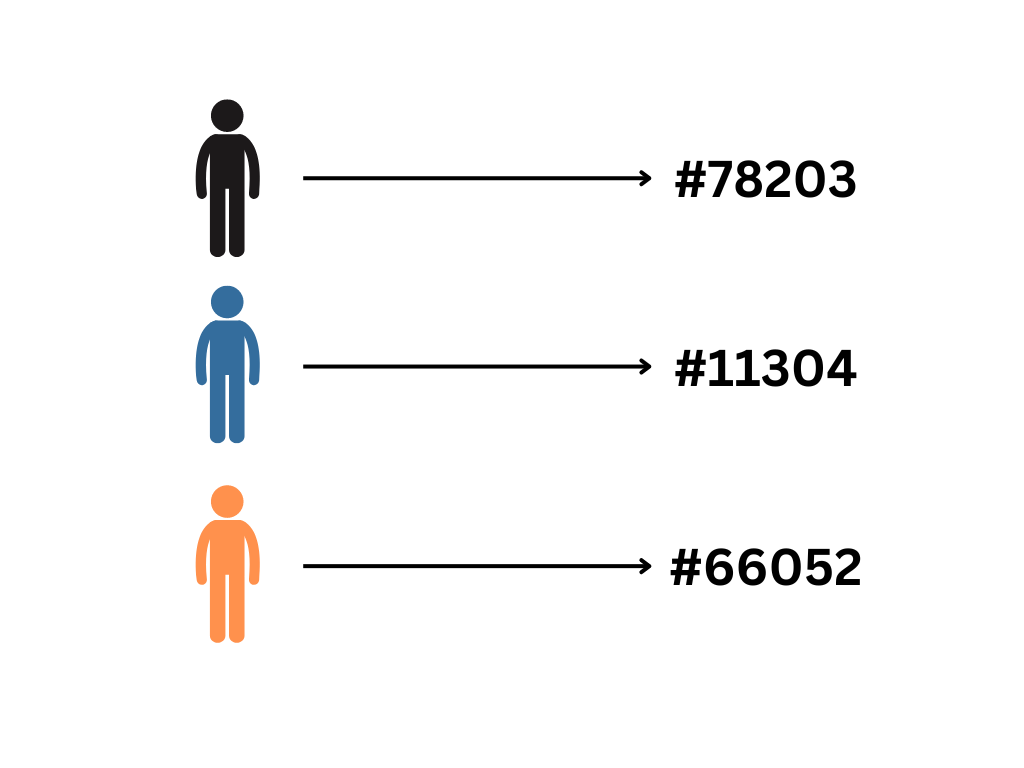
These are the simplest functions, in which each input maps to a unique output, and no two inputs share the same output. For example, imagine a school where each student has a unique ID number. Each number belongs to one student.
In this case, all elements of the input domain are mapped to a corresponding element of the output domain. However, this does not mean that all elements of the output are used; there are (many) more numbers available, so if new students are admitted they can easily get a new ID number that is not used by anybody else. In one-to-one functions, the output domain is larger (possibly infinite) than the input domain.
All-covering functions
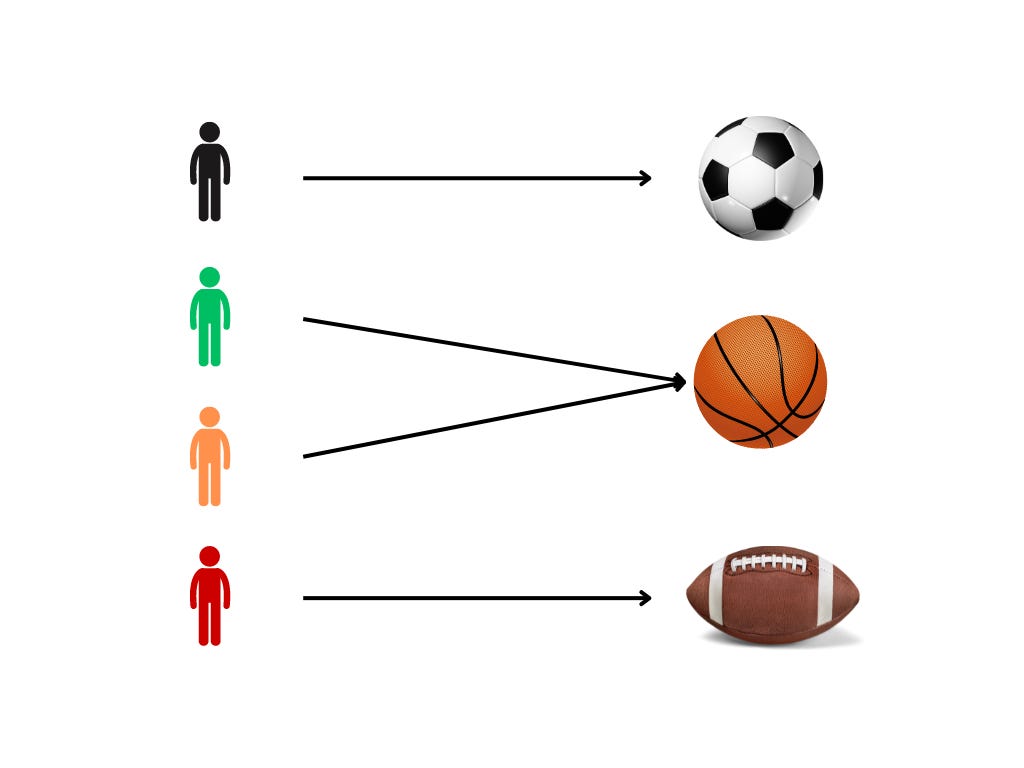
We can also have functions that cover the entire domain of output, and we can call these the ‘all-covering’ functions. Here, every element of output has a corresponding input, and multiple inputs can map to the same output. There are no unmatched outputs.
For example, imagine a group of students choosing one of the three available sports to play at their school. All sports are chosen, and some students have selected the same sport.
Two-way functions
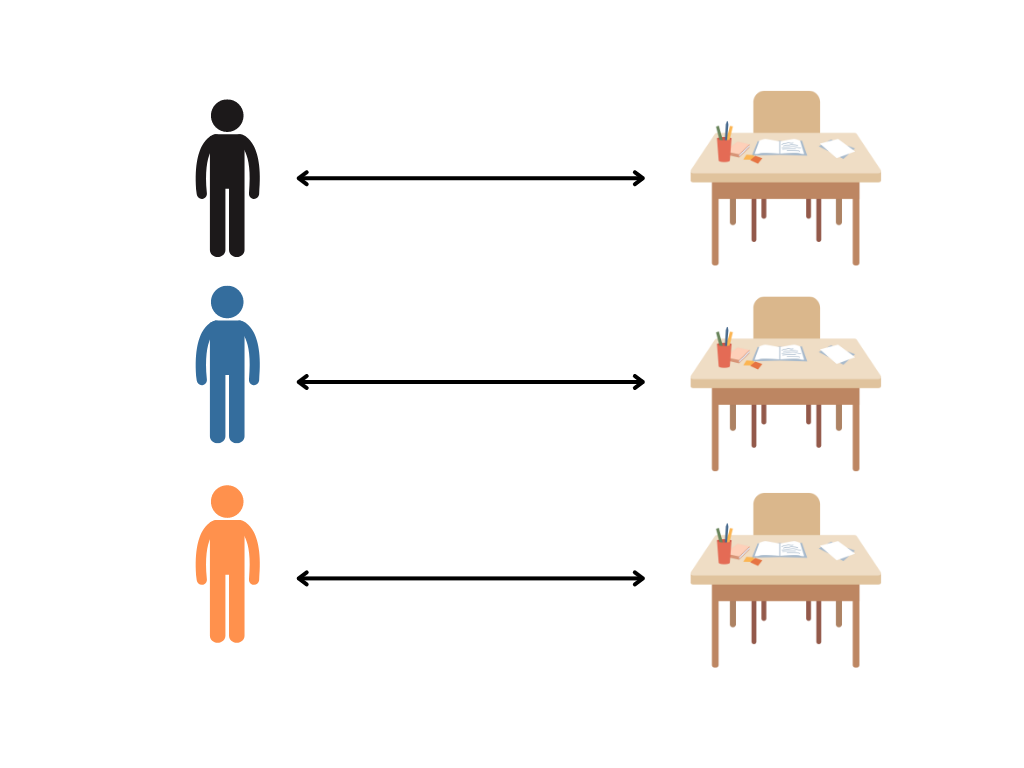
While the previous two types of functions were one-way, where one domain is possibly larger than the other, we can also have two-way functions, in the sense that there is a complete mapping between all possible elements. In these ‘two-way’ functions, there are no leftovers or doubles.
For example, if each student is assigned a desk, and there are no unused desks, and no students without one, then the mapping reflects a two-way function.
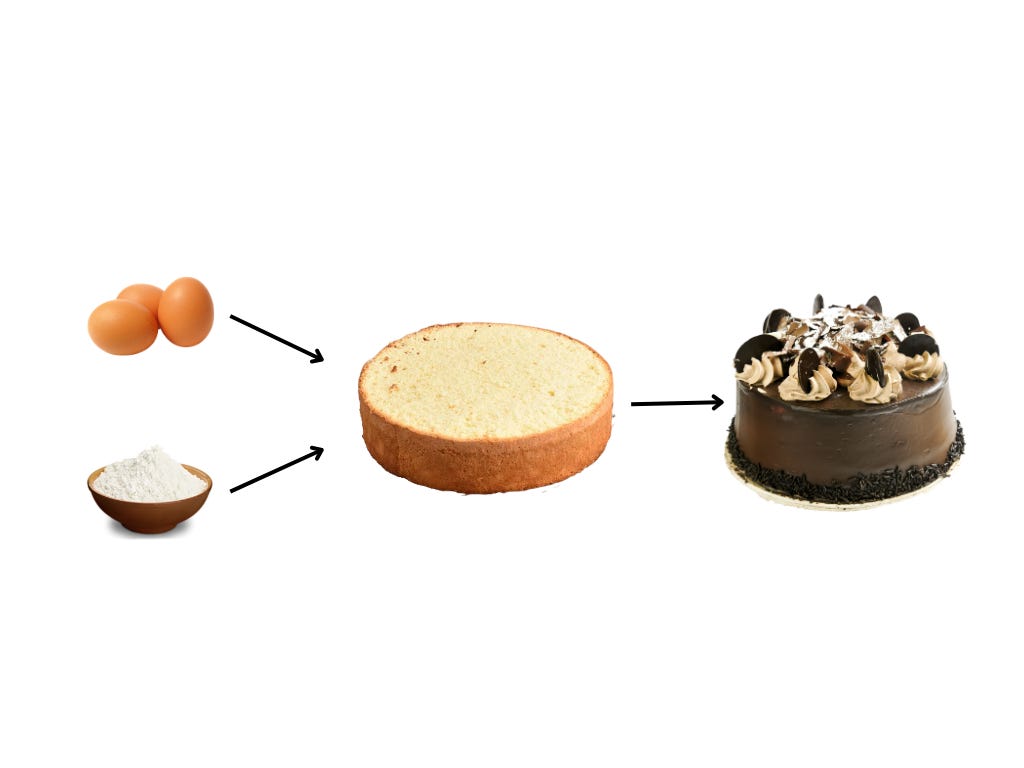
Functions of functions
Functions can also take other functions as inputs. We can call these composite, or functions of functions. In this case, the output of one function serves as the input of another, so the entire thing is like a two-step process or a layered cake.
Speaking of cakes, here is an example. A cake base without icing is the output of a function (let’s call it ‘bake’) with eggs and flour as inputs (ingredients). This output is then input to the function ‘decorate’, which produces the final, delicious output.
Exercise 2: Make a function of a function of a function. Choose any domain of initial input. Draw a graph or write a short explanation.
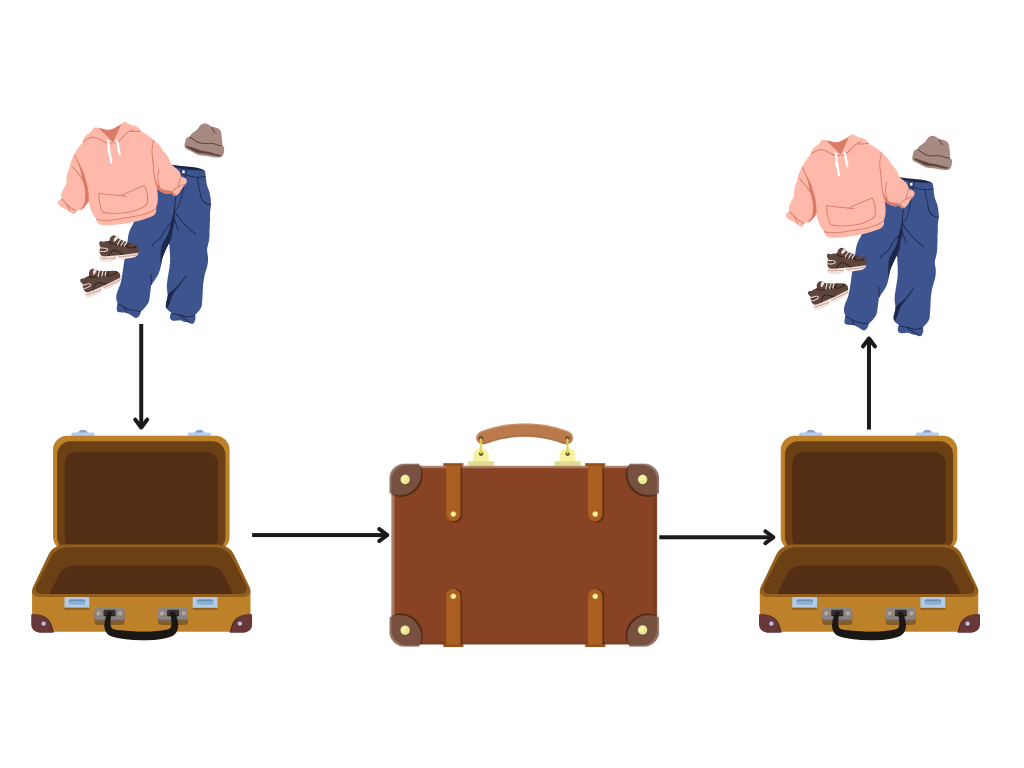
Inverse functions
Functions can also be ‘undone’ by applying inverse functions on the outputs of some other functions. If something takes you from point A to point B, an inverse function takes you back from B to A.
For example, if ‘packing the suitcase’ is an original function, then ‘unpacking the suitcase’ is its inverse: it undoes its effect.
Exercise 3: What is an inverse of an inverse function?
Why functions matter
I’m sure you realize by now why Thomas Garrity was so excited about functions because they truly are everywhere.
Philosophically speaking, a function is a model of reality (remember lesson 3?) that we create in our heads so we can understand how things interact with each other. These models can be as simple as cooking recipes, and as complex as fundamental laws of the universe.
One such function is Newton’s Second Law of Motion, which describes how the force applied to an object relates to its mass and acceleration.
Its formula is simply:
where F is the force applied to an object, m is the mass of the object and a is the object’s acceleration.
This little formula helps us understand how force, mass, and acceleration are related to one another. For example, when you push an empty shopping cart with some amount of force (F), it accelerates (a) fast because its mass (m) is not great. The same amount of force will not cause the cart to accelerate fast if the cart is full of groceries because its mass will be greater. You’ll need more F.
Functions like this one are like distillations of reality; packets of meaning that help us understand relationships between forces and objects in the world. They can help us solve problems and predict outcomes. Thanks to Newton’s function, scientists and engineers can precisely calculate how much force will be needed to send a rocket of a certain mass to space and thus how much fuel they need to pack on it.
Additionally, functions help us abstract even more from the messy reality of life and bring some order to our understanding. They do that by clearly defining the inputs, the ‘work’ the function does to the input, as well as the outputs that result. They force us to focus only on important elements and exclude irrelevant things. For example, when making a cake, you don’t need to know if the hen that laid the eggs had white or brown feathers.
The role of functions
There are two ways in which functions play a role in the world.
First, functions are end results of certain intellectual and/or research efforts. Scientists and researchers observe and measure the world to understand how it works. Their idea of how some part of the world ‘works’ is represented by a function they construct after the measurements are made.
Discovering functions in the wild
For example, if you’re an economist, you might study how the price of ice cream determines its demand (how much of it is sold). Suppose you observe the behavior of the market at one particular location (say, one particular ice cream truck in your neighborhood) and gather the following data for five different days with varying prices of ice cream:
At $1 per cone, people buy 50 cones.
At $2 per cone, people buy 40 cones.
At $3 per cone, people buy 30 cones.
At $4 per cone, people buy 20 cones.
At $5 per cone, people buy 10 cones.
You use a line chart to represent the relation between the price and demand in the following way:
You can see immediately some regularity here: the more expensive the ice cream is, the fewer people buy it. Now, if you are an owner of an ice cream truck, you’d want to know how price and demand exactly relate to one another, so you could figure out the optimal price that will make you rich.
How would you do that?
By discovering the function behind this relationship.
If we assume that the demand is the function of price, then we know that there is some function whose input is the price and the output is the demand. So, you’d have to backtrack and find how exactly these two are related by comparing the demand at each price in the data.
Fortunately, what we have here is a linear function (you can tell it’s a straight line), so you’d only have to find two things:
the slope of the line (does it go up, down, or straight?), which tells you how much and how demand changes with the price; and
the point where the line intercepts the y-axis (the left vertical line that shows the demand numbers), which tells you how much ice cream people would desire if the ice cream was free.
If the line goes upward and the slope is high, that would mean that the more expensive the ice cream is, the more people buy it. If it goes downward, it means the opposite: the more expensive it is, the fewer people buy it. A straight line indicates no difference, people buy the same amount of ice cream regardless of how much it costs.
In our case, the line goes down.
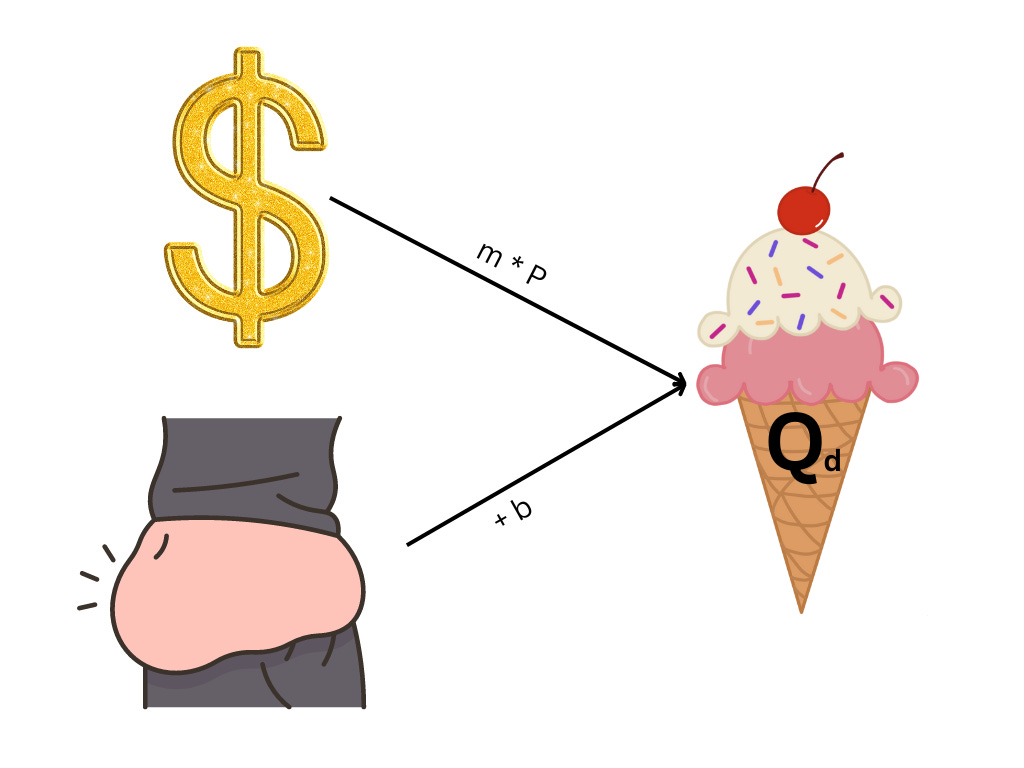
Let’s express this function as a formula, so we get more precision and order in our thinking:
If you’re unused to math formulas, or hate them, don’t fret. This one is very simple and very instructive.
Here, Q with a little d in the subscript is the Quantity of Demand, m is the slope of the line, P is the price, and b is our intercept. This formula tells us that the quantity of ice cream demanded by people is equal to price times the slope (the amount of change in demand due to price) plus the amount people want to eat ice cream in general.
Pause a bit to think if this makes sense to you.
Think about it this way: How much ice cream people want to buy every day does seem determined by both the price and some innate desire to eat ice cream. Even if ice cream were free, you’d only want to eat so much ice cream every day. Although that is hard to believe, there is too much ice cream after all.
The fancy math formula of this function can also be expressed in this way:
How can we figure out the parameters (the ‘working engine’) of this function, m and b? Turns out it is quite easy. First, we find the slope m by dividing the change in quantity of demand by the change in price.
Here’s the formula, if you insist:
Here, the big triangle symbol is a capital Greek letter delta, usually used to signify change in some quantity. This is nothing more than a difference between two subsequent data points, where we subtract the first from the second one.
Let’s use two points to calculate the slope. If we take the subsequent points ($1.00, 50) and ($2.00, 40) for the number of ice creams sold at these prices, we get:
Our slope m is -10. We can now plug this value of m into our function formula to solve for b using the point ($1.00, 50):
And there it is! Now, we have the parameters of our function and we can actually interpret the relation between the price and the demand for ice cream.
Since the intercept b indicates the default desire for ice cream, we can say that at this particular ice cream truck, people would eat 60 cones a day if the ice cream was free. The slope indicates the rate at which demand changes with the price, so we can say that for every $1 increase in the price, the quantity demanded (and sold) decreases by 10 units.1 You can verify that even visually, if you look at the line chart carefully.
Isn’t this amazing?
Do you see how this function breaks down a complex relationship between two phenomena in the world and helps us understand them better?
I hope you do.
Functions like these are the workhorse of science, engineering, and overall human progress. They are amazing conceptual devices that allow us to tame nature, at least a bit.
Functions as play
The second way functions play a fundamental role in knowledge is in giving us tools to play, or to use a more serious word: to experiment.
Namely, we don’t have to only look for functions that describe the real world. We can also make functions on our own, define them in any possible way we want, and observe what happens as a result.
Let’s make some functions
We are going to play now. It is time to have some fun making functions with Python. If you remember the last lesson, Python is an amazing programming language that allows us to do many things. Making custom functions and running them to see the results is one of those things.
So, let’s go to Google Colab, open a new notebook, and start making some functions.
In Python, we can think of functions as blocks of code that perform a specific task. Think of them as written recipes that produce the desired result. As in a recipe, we need two things: ingredients (inputs, also called arguments or parameters), and the steps (the code inside the ‘body’ of the function) that need to be performed.
There are two terms you have to remember: first, when we design a function, we define it; second, when we use the function, we call it. These are two different procedures. Functions are defined only once, but they can be called (used) as many times as you want.
In Python, we define a function by using the def keyword, followed by the function name and parentheses (which contain the function’s parameters) and a colon.
Here’s the basic structure:
Again, note the indentation. All the code within the function needs to be indented in one place. Also, note the return word. If we want our functions to produce an output, we need to use this command.
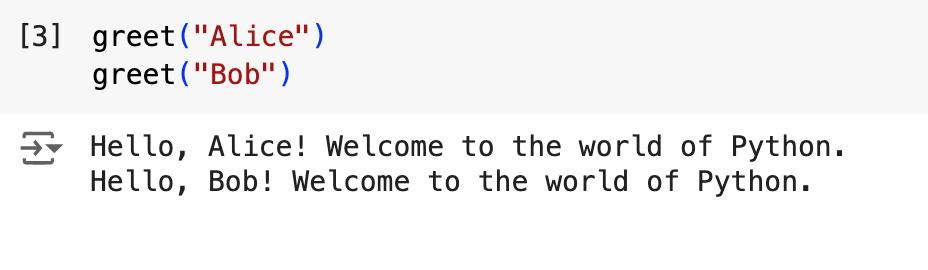
Let’s make a simple function that prints a greeting:
This function is called greet and takes just one parameter, name. The function prints the text we assign to it and inserts whatever the user of the function puts in as the parameter.
You recall strings from the last lesson, I hope. They are letter or word data types specified by single or double quotation marks. What we have here is a special kind of string called an ‘f-string’ because it is prefaced by a letter f which allows us to insert a variable within the string (specified by the curly brackets).
Now, when the user calls this function, they do it like this:
Any possible string can be used with this function. It is reusable and flexible. Try it out yourself.
Functions can take more than one parameter. Here’s one that adds two numbers:
Notice here that I could have put the print instead return command in the body of the function. I chose not to do that because I can then use this function for other kinds of computation; the output stays in the function’s memory.
Check it out:
Here, I’m using one function that I defined before inside a new function. When I call the function, I get the desired result.
Exercise 4: Define a functiongreet_2that takes two inputs,nameandday, and prints: "Hello ___, today is ___." where name and day are variables the user can choose.
Exercise 5: Define a functioncelsius_to_fahrenheitwith one parameter (the temperature in Celsius) that returns the temperature in Fahrenheit. Find the exact mathematical function on the internet. Note: division symbol is/and multiplication symbol is*in Python. You can use brackets as you would in ordinary math calculation.
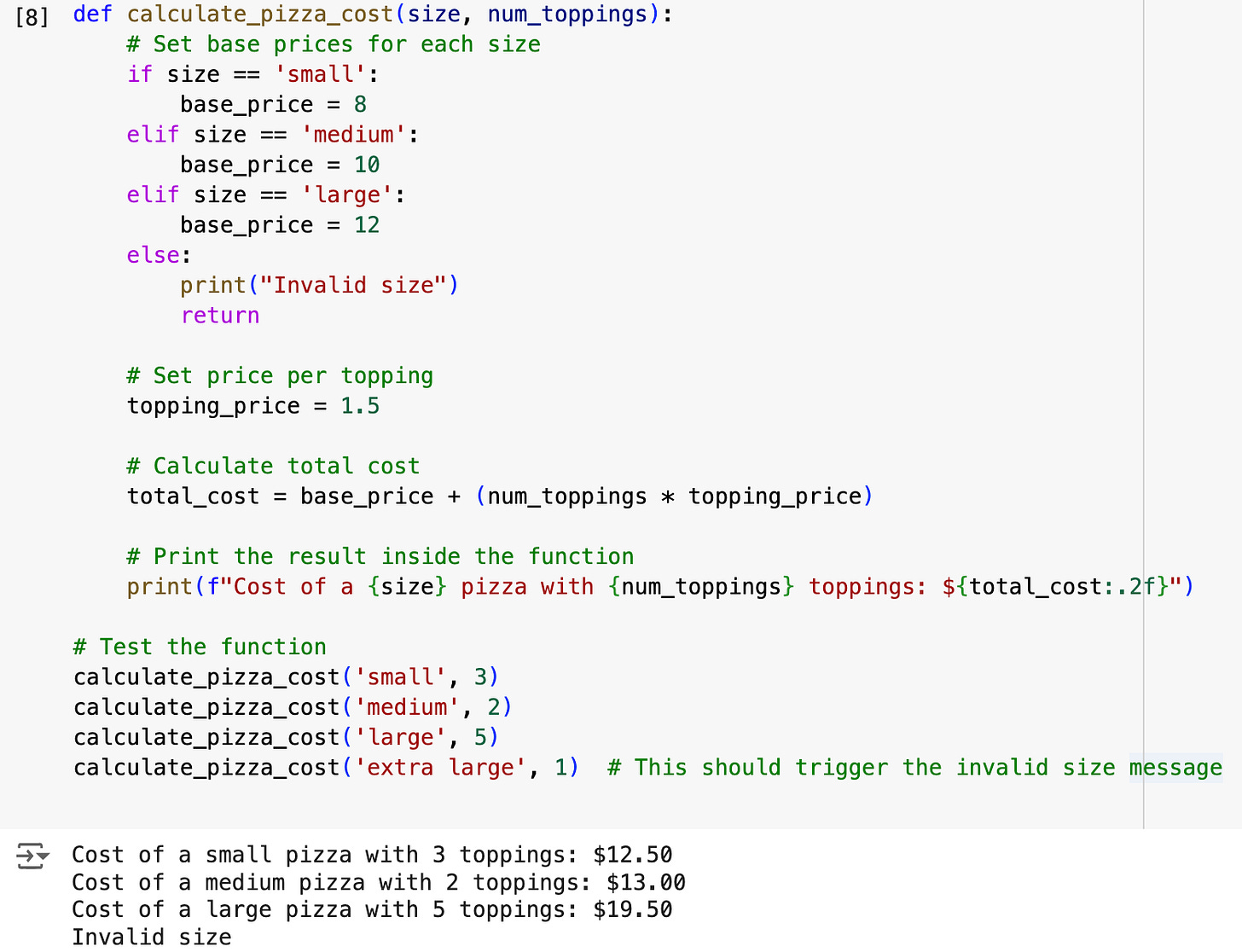
Let’s do one more example. Imagine that you are the owner of a small pizzeria and you wish to write a function that will calculate the price of different types of your pizzas, which vary by size and the toppings included.
Here’s how you could do it:
Let’s go through it. First, the green letters prefaced by # are called comments, and they don’t affect the code at all. Any line of code, when prefaced by # will not do anything. These are just helpful comments that tell you what each piece of function does.
You can see that the function takes two parameters. These would be inputs you (or your cashiers at the pizzeria) would use when calling the function.
In the first several lines we use the conditional commands (that we covered in the last lesson). Notice the else command at the end of this block: it tells Python what to do in case the user enters some other value for the pizza size: print “Invalid size.”
Next, we set the topping price at $1.50 and calculate the total cost of the pizza by adding the base price to the multiple of the topping price and the number of toppings. We then print a sentence with the number of toppings and the pizza price. The :.2f code in the total_cost variable determines how many decimal places we want to be printed, in this case just two.
Exercise 6: Define a function called classes_today that will take one input, the day of the week, and print what classes you have on that day (if no classes, print 'None'). Use the conditional commands like in the pizza example.Wrap up
Functions are important elements of any sophisticated thinking about the world. If you understand them well, you’ll be able to see them everywhere around you. Moreover, they can help you interact with the world in more efficient ways. You can use them to make predictions, devise plans, and execute actions that will be beneficial for you.
We will use a lot of the knowledge and concepts we have covered today in future lessons, so stay tuned. I also hope this awoke your interest in functions. If it did, go hug your loved ones and tell them all about functions.
As usual, I will leave you with a reading suggestion.
Here’s a book which will teach you a lot about functions. It is about the ‘mathematics of mathematics’, or about the conceptual apparatus that lies behind mathematical reasoning. It’s a math book with almost no numbers!
Cheers!
Of course, no measurement is perfect and there’s always something data scientists call ‘noise’, which is an error in measurement. In the real world, our function would have to include this noise (which is not too big if the measurements are done properly).